编辑距离 | My Front End Blog

题目链接：
https://leetcode-cn.com/problems/edit-distance/

定义 dp[i][j] 的含义为：word1 的前 i 个字符和 word2 的前 j 个字符的编辑距离。意思就是 word1 的前 i 个字符，变成 word2 的前 j 个字符，最少需要这么多步。

边界：如果其中一个字符串是空串，那么编辑距离是另一个字符串的长度。比如空串 “” 和 “ro” 的编辑距离是 2（做两次“插入”操作）。再比如 “hor” 和空串 “” 的编辑距离是 3（做三次 “删除” 操作）。

状态转移：
对于每对字符 s1[i] 和 s2[j]，可以有四种操作：

if s1[i] == s2[j]:
    啥都别做（skip）
    i, j 同时向前移动
else:
    三选一：
        插入（insert）
        删除（delete）
        替换（replace）

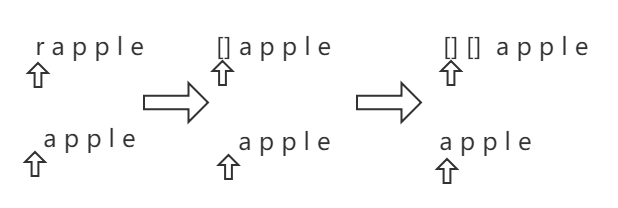
word1 执行插入操作：在 s1[i] 插入一个和 s2[j] 一样的字符，那么 s2[j] 就被匹配了。然后移动 j，让 i 和下一个 j 匹配。dp[i][j] = dp[i][j - 1] + 1
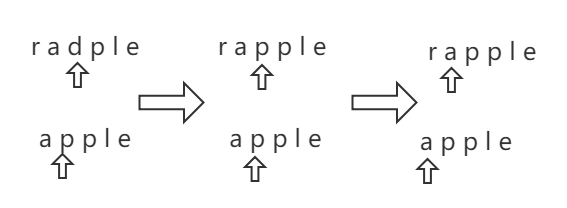
word1 执行删除操作：直接把 s1[i] 字符删除，那么 s2[j] 就被匹配了。然后继续移动 i，让新的 i 与原来的 j 匹配。dp[i][j] = dp[i - 1][j] + 1
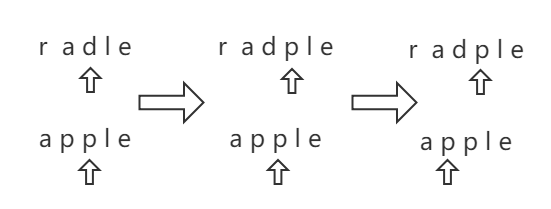
word1 执行替换操作：直接把 s1[i] 替换成 s2[j]，这样它们就匹配了。然后 i 和 j 同时移动，进行下一个字符的比较。dp[i][j] = dp[i - 1][j - 1] + 1

/**
 * @param {string} word1
 * @param {string} word2
 * @return {number}
 */
var minDistance = function(word1, word2) {
    const m = word1.length, n = word2.length;
    const dp = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));

    // 边界
    for (let i = 1; i <= m; i++) {
        dp[i][0] = i;
    }
    for (let j = 1; j <= n; j++) {
        dp[0][j] = j;
    }

    // dp
    for (let i = 1; i <= m; i++) {
        for (let j = 1; j <= n; j++) {
            if (word1[i - 1] === word2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1];
            } else {
                dp[i][j] = Math.min(dp[i][j - 1] + 1, dp[i - 1][j] + 1, dp[i - 1][j - 1] + 1);
            }
        }
    }

    return dp[m][n];
};

参考题解：