全排列 | My Front End Blog

题目链接：
https://leetcode-cn.com/problems/permutations/
解法分析：
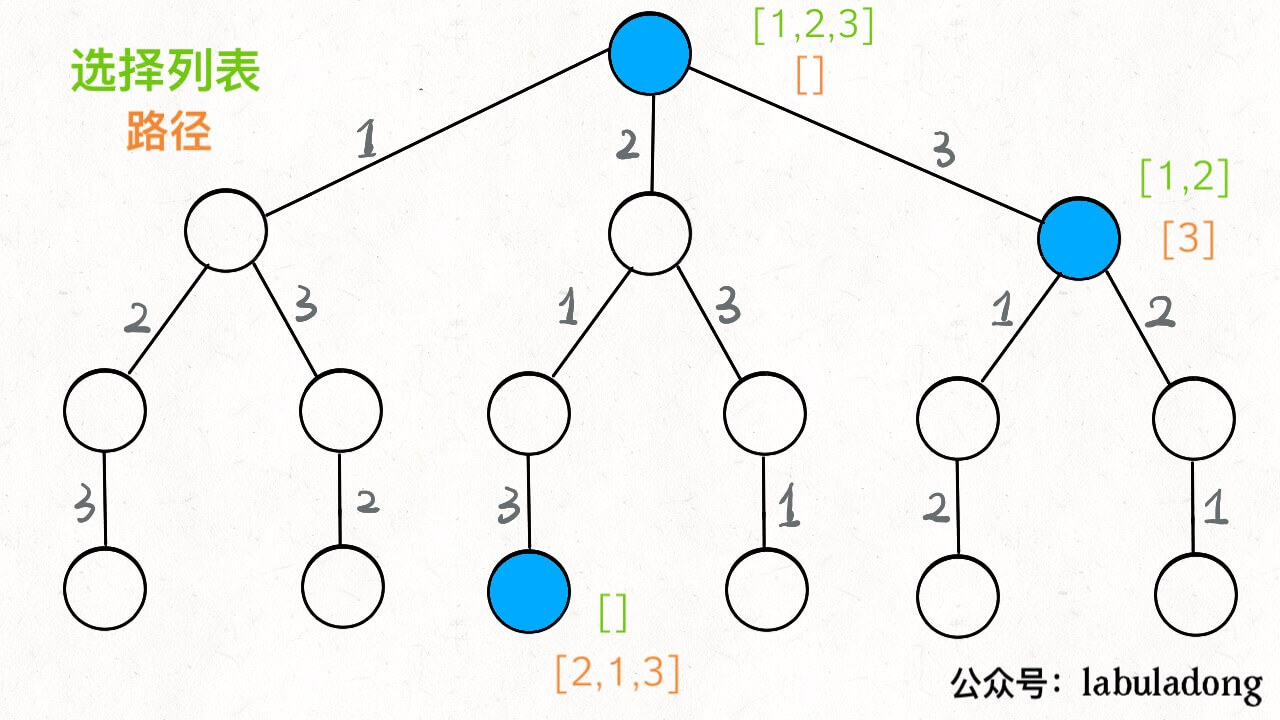
解决一个回溯问题，实际上就是一个决策树的遍历过程。只需要思考 3 个问题：

路径：也就是已经做出的选择
选择列表：也就是你当前可以做的选择
结束条件：也就是到达决策树底层，无法再做选择的条件

比如：

回溯的通用解法:

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

核心可以用一句话总结：在递归之前做出选择，在递归之后撤销刚才的选择。

/**
 * @param {number[]} nums
 * @return {number[][]}
 */
var permute = function(nums) {
    const res = [];
    const set = new Set(); // set 用于记录是否访问过，也可以开一个 vis 数组标记
    backtrack([]);
    return res;

    function backtrack(path) {
        // 回溯边界
        if (path.length === nums.length) {
            res.push(path.concat());
            return;
        }

        for (let i = 0; i < nums.length; i++) {
            if (!set.has(i)) {
                path.push(nums[i]); // 做选择
                set.add(i); // 标记

                backtrack(path);

                path.pop(); // 撤销选择
                set.delete(i); // 取消标记
            }
        }        
    }
};

参考题解：